我信概最后写了个什么"从序列维护到动态图的数据结构概述"然后只拿了3.0,果然是傻逼课,建议大家转专业的话别选这个课。
T1:そらのおとしもの(Version2)
Idea:lxl Solution:lxl Std:lxl Data:lxl
https://www.luogu.org/problem/P5397
http://www.51nod.com/Challenge/Problem.html#problemId=2046
"弑尽破净的第四分块" (妈呀这名字好中二啊(谁叫我要用日本轻小说中的东西命名真是作死))
这题就是我想改一个已有的经典根号形式改出来,然后想了想发现可以做
考虑根号分治
定义一个值x出现次数为size[x]
如果没有修改操作,则预处理所有size大于$ \sqrt n$的值到所有其他值的答案,以及每个值出现位置的一个排序后的数组
查询的时候如果x和y中有一个是size大于$ \sqrt n$的,则可以直接查询预处理的信息,否则进行归并
$O( n \sqrt n + m \sqrt n )$
有修改操作即在这个做法上改良,因为发现这个做法的根号平衡并没有卡满,所以有改良余地
假设把所有x变成y
由于可以用一些技巧使得x变成y等价于y变成x,所以不妨设size[x] < size[y]
定义size大于$ \sqrt n$为大,size小于等于$ \sqrt n$为小
定义ans[x][y]为x到y去除附属集合的部分的答案(附属集合是什么下面有说)
x取遍所有值,y只有所有大的值,总$O( \sqrt n )$个
修改:
如果x和y均为大,则可以暴力重构,$O( n )$处理出y这个值对每个其他值的答案,因为这样的重构最多进行$O( \sqrt n )$次,所以这部分复杂度为$O( n \sqrt n )$
如果x和y均为小,则可以直接归并两个值的位置的排序后的数组,单次$O( \sqrt n )$,所以这部分复杂度为$O( m \sqrt n )$
如果x为小,y为大,发现小合并进大的均摊位置数为$O( n )$,对这个再次进行根号平衡
对于每个大,维护一个附属的位置集合,这个位置集合的大小不超过$O( \sqrt n )$
每次把小的x合并入大的y的时候,即合并入这个附属集合,并且用x到所有大的值的答案更新y到所有大的值的答案,这样
如果合并后附属集合大小超过$O( \sqrt n )$,则$O( n )$重构y到所有值的答案,这个过程最多进行$O( \sqrt n )$次,均摊复杂度$O( n \sqrt n )$
由于大的值个数$ \le \sqrt n$ , 附属集合大小$ \le \sqrt n$,这一部分是单次$O( \sqrt n )$的,所以这部分复杂度为$O( m \sqrt n )$
查询:
如果x和y均为大,则在维护的答案中查询min( ans[x][y] , ans[y][x] ),然后将x的附属集合和y的附属集合进行归并,这一部分是单次$O( \sqrt n )$的,所以这部分复杂度为$O( m \sqrt n )$
如果x和y均为小,则进行一次归并即可,所以这部分复杂度为$O( m \sqrt n )$
如果x为小,y为大,则在维护的答案中查询ans[x][y],然后将x和y的附属集合进行归并,这一部分是单次$O( \sqrt n )$的,所以这部分复杂度为$O( m \sqrt n )$
由于维护了所有可能的贡献,而且更新是取min,正确性也得到了保障
时间复杂度$O( (n+m) \sqrt n )$,空间复杂度$O( n \sqrt n )$
存在序列分块做法
对这题的评价:6/11

T2:ゴシック(Version2)
Idea:lxl Solution:lxl Std:lxl Data:lxl
https://www.luogu.org/problem/P5398
https://cometoj.com/problem/1072
"点缀光辉的第十四分块" (妈呀这名字好中二啊(谁叫我要用日本轻小说中的东西命名真是作死))
这题是我研究区间逆序对之后,枚举了一些区间pair贡献的题里面的一个
最开始枚举出来的时候我只会$O( n^{1.5+\epsilon } )$的暴力做法(实际上在n=1e5的范围内接近于$O( n^{7/4} )$),然后过了一年再看到这题就会了......
我们考虑莫队维护,不失一般性这里只讨论莫队的四种拓展方向里面的一种
每次把区间$[l,r]$拓展到$[l,r+1]$的时候需要维护$a[r+1]$和$[l,r]$这段区间的贡献
这里利⽤莫队二次离线的trick:
莫队就可以抽象为&n \sqrtm&次转移,每次查询一个序列中的位置对一个区间的贡献
这个贡献是可以差分的, 也就是说把每次转移的$a[r+1]$对区间$[l,r]$的贡献差分为$a[r+1]$对前缀$[1,r]$的贡献减去对前缀$[1,l-1]$的贡献
然后通过这个差分我们可以发现,我们把$O( n \sqrt m )$次的修改降低到了$O( n )$次修改,因为前缀只会拓展$O( n )$次
于是我们每次可以较高复杂度拓展前缀和,因为插入次数变成了$O( n )$次
然后这⾥我们离线莫队的转移的时候可以做到线性空间,因为每次莫队是从一个区间转移到另一个区间:
我们记下$pre[i]$为$i$的前缀区间的答案,$suf[i]$为$i$的后缀区间的答案
不失一般性,只考虑把区间$[l1,r1]$拓展到区间$[l1,r2]$:
$[l1,r1]$区间的答案为红色部分的贡献,$[l1,r2]$区间的答案为红色部分加上绿色部分的贡献,$r2$的前缀贡献为所有的贡献,$r1$的前缀贡献为红色的贡献与前两个蓝色的贡献
于是我们可以把绿色的贡献,也就是两次询问的差量差分为$pre[r2]-pre[r1]-${$[1,l1-1]$对$[r1+1,r2]$的贡献}
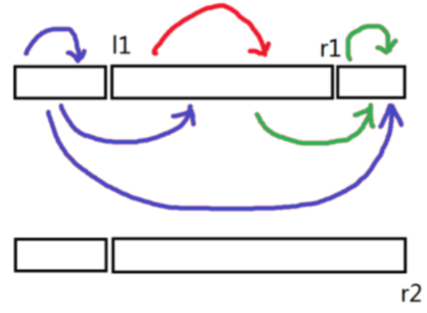
然后我们再差分⼀下$[1,l1-1]$对$[r1+1,r2]$的贡献为$[1,l1-1]$对$[1,r2]$的贡献减去$[1,l1-1]$对$[1,r1]$的贡献,这里每个位置开个vector存⼀下就可以了
于是我们达成了$O( n + m )$的空间复杂度将莫队给⼆次离线
现在考虑怎么算这个贡献,我们要高效计算区间$[l,r]$对$x$的贡献时
先把贡献拆开变成:$[l,r]$中$x$的倍数个数,$[l,r]$中$x$的约数个数
$[l,r]$中$x$的倍数个数:每次前缀加入一个数$a_i$的时候,我们把$a_i$的约数位置所对应的数组$pre1$的位置都++
然后查询的时候直接查$pre1[x]$即可得到$x$倍数个数
$[l,r]$中$x$的约数个数:这里考虑对$x$的约数进行一次根号分治
对于所有$x$⼤于$\sqrt n$的约数,我们拓展前缀的时候维护,即每次把$a_i$的倍数位置所对应的数组$pre2$的位置都++
然后查询的时候直接查$pre2[x]$即可得到$x$大于$\sqrt n$的约数个数
对于所有$x$小于$\sqrt n$的约数,我们考虑每次直接枚举区间$[l,r]$中$1,2,...\sqrt n$的出现次数
这里可以先枚举$1,2,...\sqrt n$,然后预处理一个前缀和,$O( n + m )$算出对每个询问的贡献,从而节省空间
于是我们得到了⼀个总时间复杂度$O( n( \sqrt n + \sqrt m ) )$,空间$O( n + m )$的做法
对这题的评价:8/11

T3:駄作(Version1)
Idea:lxl Solution:ccz Std:ccz Data:ccz
https://www.luogu.org/problem/P5399
https://loj.ac/problem/6612
"????的第七分块" (不中二了)
这个是我在军训走路的时候想出来的东西,然后我不会做,但是ccz会做
最开始给的做法是在静态top tree上跑莫队二次离线什么的,后面发现存在直接分块而不利用分治的做法,所以这题变简单了很多
这里只给出树分块做法,并不给出树分治做法
对于树上的顶点 $a,b$,顶点集 $S,S1,S2$,定义 $d(a,b)$表示顶点 $a$ 到 $b$ 的距离,若 $a=b$ 则 $d(a,b)=0$,否则 $d(a,b)$是 $a,b$ 间简单路径的边数;
另外定义
$d(S,a) = d(a,S) = ∑ d(a,b)[b∈S]$
$d(S1,S2) = ∑ d(a,S2)[a∈S1]$ 。
树 $T$ 上的一个邻域 $NT(x,y)$定义为到顶点 $x$ 距离不超过 $y$ 条边的顶点集。$x$ 称为邻域的中心, $y$ 称为邻域的半径。
真实的树分块——Topology Cluster Partition(名字正确性存疑)
树分块将 n 个结点的树分成了一些块的并,满足下列性质:
1.每个块是树
2.每个块中有两个特殊的点,称为端点 1 和端点 2。
3.不同块的边集不相交
4.一个块中的顶点,除端点外,其余顶点不在其它块中出现
5.如果一个顶点在多个块中出现,那么它一定是某一个块的端点 2,同时是其余包含这个顶点的块的端点 1
6.如果把所有块的端点作为点,每块的端点 1 和端点 2 连有向边,则得到一棵有根树
这里给出树分块的一个实现,满足块数和每块大小均为 $O( \sqrt n )$:
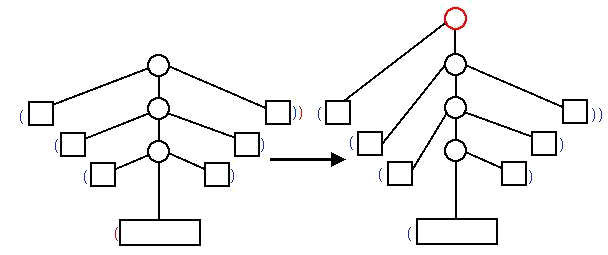
在有根树中,每次选一个顶点 $x$,它的子树大小超过$\sqrt n$,但每个孩子的子树大小不超过$\sqrt n$, 把 $x$ 的孩子分成尽可能少的块(以 $x$ 为端点 1,但暂时允许有多个端点 $2$,且每块至多有 $2 \sqrt n$ 个顶点),然后删掉 $x$ 的子树中除 $x$ 外的部分。重复直到剩下的点数不超过$\sqrt n$,自成一块。 这样就求出一个保证块中顶点数和块数均为 $O( \sqrt n )$的树分块(块间可以共用一些顶点,但每条边只属于一个块),如果一个块有多个端点(即被多个块共用的点),则在块内将这些端点建出虚树,将虚树上的每条边细分为一个新的块,以保证最终每个块只有两个端点。
如果只有单次询问,可以进行转化:
$d(S1,S2) = ∑[d(a,c)*|S2|+d(b,c)*|S1|−2d(lca(a,b),c)][a∈S1,b∈S2]$,其中 $c$ 是任意一个点。这里我们取$c$为根节点,这样把两两顶点间的距离和转化为了点集内顶点的深度和以及两两顶点间 lca 的深度和:
$d(S1,S2) = ∑[dep(a)*|S2|+dep(b)*|S1|−2dep(lca(a,b))][a∈S1,b∈S2]$
对 lca 部分可以在$ O(n)$时间内求出:初始化树的边权为 $0$,将 $S1$ 中的每个顶点到根的路径的边权$+1$,求 $S2$中每个顶点到根的路径的边权和之和。
首先进行树分块,方便起见,认为一个块包含块中除了端点 $1$ 之外的点,这样每个点就恰好属于一个块。 预处理每个块 $B$(端点为 $a1,a2$)中的 $d(NB(ai,x),aj)(i,j=1,2)$,需要 $O(n)$时间和空间。
树 $T$ 的一个邻域可以拆分为这个邻域和每个块的交。
对于块 $B$,若 $x$ 在 $B$ 中,则 $NT(x,y)∩B=NB(x,y)$; 否则设 $z$ 是 $B$ 中距离 $x$ 较近的端点,距离为 $d$,则 $NT(x,y)∩B=NB(z,y-d)$。
求两个邻域间的距离和,只需考虑这两个邻域和每个块的交。求块 $B1,B2$ 的两个邻域 $n1=NB1(x1,y1)$和 $n2=NB2(x2,y2)$间的距离和。 如果 $xi$ 不是 $Bi$ 的端点,则显式地求出 $ni$ 以及 $ni$ 到 $Bi$ 的端点的距离和,这需要 $O( \sqrt n )$的时间。
当 $B1≠B2$ 时,设 $a$ 为 $B1$ 中最靠近 $B2$ 的端点,$b$ 为 $B2$ 中最靠近 $B1$ 的端点,$n1$ 和 $n2$ 间的距离和 $d(n1,n2)=d(a,b)*|n1|*|n2|+d(n1,a)*|n2|+d(n2,b)*|n1|$。通过在块构成的树上 dfs,这部分可以在 $O( \sqrt n )$时间内处理。
当 $B1=B2$ 时,如果 $x1$ 和 $x2$ 都是 $B1$ 的端点,每块每次询问这种情况出现至多 $1$ 次,这里暂不考虑,最后再离线处理;否则每次询问这种情况只出现 $O(1)$次,可以 $O( \sqrt n )$暴力处理。
离线处理的部分,枚举每个块 $B$,再枚举询问(只需考虑两个邻域的中心都不在 $B$ 中的询问) 计算贡献,有 $O(n)$个询问形如 $d(NB(a,y1),NB(b,y2))$,对<$a,b$>的 $4$ 种情况分别计算。由于块中 点数的限制,<$y1,y2$>实际只有 $O(n)$种($y1,y2=O( \sqrt n )$)。 仍然转化为求两两点间 lca 的深度和,枚举 $y1$,维护初始边权为 $0$,将 $NB(a,y1)$中每个点到 根路径上的边权$+1$ 后得到的树,此时每个 $y2$ 对应的答案是 $NB(b,y2)$中每个点到根的路径的边权和之和。这部分时间和空间都是 $O(n)$的。
时间复杂度$O( (n + m)\sqrt n )$,空间复杂度$O( n+m )$
最后推荐一下这个gal,挺好玩的
对这题的评价:10/11










 鄂公网安备 42010202000505 号
鄂公网安备 42010202000505 号