T1：帰らぬ者と、待ち続けた者たち（Version?）

Idea：kcz Solution：kcz/lca Std：kcz/lca Data：kcz

https://www.luogu.org/problem/P5065

将原序列分成k块，每个块维护块内每个长度下or的最大值

修改时，块内暴力重新计算每个长度下or的最大值，就是枚举右端点，然后到他的or和不同的左端点只有log种，枚举就可以了 时间复杂度$O(n/k \times log(n))$

询问时，答案在块内的情况: check每个块，如果可以把答案减少$1$，就更新答案，然后重复操作，否则退出 时间复杂度$O(k+n/k)$

如果答案跨过块，则从左到右枚举块，同时维护块左边所有不同的后缀or和 具体就是从一个块到下一个块的时候，把所有不同的后缀or和都or上自己整个块的or和，然后再加入自己所有不同的后缀or和(提前维护好)。之后去一下重 时间复杂度$O(k \times log(n))$

现在考虑答案右端点在块内，左端点在块左边的情况，然后从左到右枚举块内所有不同前缀or和(提前维护好) 如果他跟 当前最大的在块前面的后缀or和 的or和大于等于$k$，就更新答案并删除当前最大的在块前面的后缀or和，然后重复操作 否则退出。 时间$O(k \times log(n))$

$k$取$\sqrt n$时，

总时间复杂度$O(m sqrt(n) log(n))$

用一个线段树维护每个节点每种前缀 or 和以及每种后缀 or 和，然后暴力算出这两者一一对应的最优 or 和

再用一组堆维护每种长度上述所有的 or 和，再用一棵线段树维护每种长度 or 和的最小代价。查询时二分即可。

时间复杂度$O( mlog^2nlog^2a )$，其中修改一次的复杂度为$O( log^2nlog^2a )$，查询一次的复杂度为$O( logn )$，但是感觉平衡只能去掉$polyloglog(n)$，难以去掉log

对这题的评价：3/11

T2：誰も彼もが、正義の名のもとに（Version5）

Idea：lxl Solution：lxl Std：lxl Data：lxl

https://www.luogu.org/problem/P5066

考虑用平衡树维护序列，将一段连续的同色极长段缩为一个点

发现操作具有对称性，本质上只有

区间染色为0/1

区间每个数or/and上左/右

区间和

这三种操作

发现第二种操作其实就是让区间中0/1的同色极长段各自向左/右扩散一格的位置

我们修改的时候不修改这个给定的区间，而是让区间两端点根据操作种类和所在的同色极长段的颜色进行调整，具体来说就是检查一下是否包含这个同色极长段，然后调节我们这次修改的区间的位置

然后问题便转化为，每次区间中0/1的同色极长段各自变大1或者缩小1，这个可以通过在缩点平衡树结构上打标记来实现

因为有可能一个同色极长段在缩了之后变成0，所以我们需要维护一下区间内最小的同色极长段长度，如果是0则暴力将其删去，同时合并两边的段

可以发现每次修改只会增加$O(1)$个同色极长段，每次删除可以花$O( logn )$的代价减少一个同色极长段

总时间复杂度$O( (n+m)logn )$，空间复杂度$O( n )$

对这题的评价：4/11

T3：消えない過去、消えていく未来（Version?）

Idea：mcfx Solution：mcfx Std：mcfx Data：mcfx

https://www.luogu.org/problem/P5067

题解 为了描述简洁，以下均用 $K$ 指代括号层数。

由于长度和操作次数同阶，以下均用 $N$ 指代这两个量。

算法 1

考虑用一棵树存储整个串。

查询时类似线段树或平衡树的区间查询。

对于第一个部分分，这棵树需要有 + - * 和数字几种节点。

+ 和 - 节点由于运算优先级相同，可以一起处理。

为了满足运算优先级的要求，需要数字节点的深度 > * 节点的深度 > + - 节点的深度。

显然，这样一棵树是非常容易构建的，可以直接当成非旋转 Treap，在合并操作时判断一下优先级即可。

时间复杂度：$O(N log N)$。

空间复杂度：$O(N)$。

期望得分：10 分。

算法 2

加上括号后，需要一种新的节点表示括号。

这里我们定义一种新节点 () ，表示一对括号。每个 () 节点有三个儿子，左儿子、右儿子和中儿子，左儿子和右儿子的含义与其他节点相同，中儿子表示括号内的表达式。 () 节点和其他节点合并时，优先级与数字节点相同。 对于不成对的括号，可以在原串最左边添加若干 ( ，最右边添加若干 ) 配成对，添加的括号显然是 $O(N)$ 的。

现在问题是如何构建一棵满足条件的树。

对于一个括号合法的表达式，可以从左往右扫一遍，用栈维护当前每层括号内的表达式。

当一对括号闭合时，添加一个 () 节点，中儿子指向内部的根，再与上一层合并即可。

查询时需要特判区间只包含一边括号的情况。

时间复杂度：$O(N log N ⋅ K)$。

空间复杂度：$O(N)$。

期望得分：20 分。

算法 3

考虑没有括号，但是有修改操作的情况。

当修改后的运算优先级不变时，可以直接修改。

如果修改后的运算优先级发生改变，可以先把该节点和左右的表达式分裂，修改完再合并到一起，这个可以用非旋转 Treap 很容易的实现。

时间复杂度：$O(N log N)$。

空间复杂度：$O(N)$。

期望得分：30 分，与算法 2 结合可得 40 分。

算法 4

如果同时有括号和修改，可以沿用算法 2 中树的结构。

对于修改操作，如果被修改的不是括号，可以与算法 3 类似的处理。不过这里只需要和最内层括号内的表达式分裂、合并。

如果修改了括号，可以把每个操作分解为若干个下列操作：

1.加入一个括号；

2.删除一对括号；

3.加入或删除一个其他节点。

第三种操作可以直接在 Treap 上处理。

第二种操作只需要把左节点、中节点、右节点依次合并即可。

对于第一种操作，多了一个不成对的括号，可以视为在无穷远处加了一个方向相反的括号。

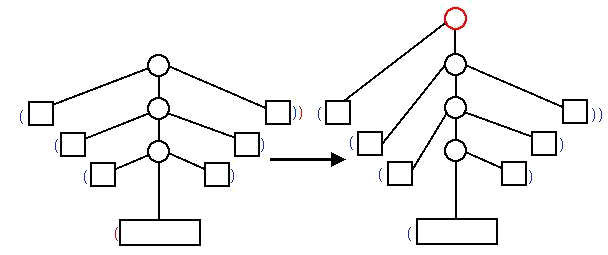
如图，左边表示操作前树的形态，右边表示操作后的。圆点表示 () 节点，方点表示其他节点，圆点下方连接的节点表示括号内的内容。蓝色括号表示实际的括号位置，红色括号表示新加入的括号。

加入这两个括号后，需要新加入一个 () 节点，然后把每层括号的一侧分裂，然后合并到上一层。这个过程可以从上到下递归实现。

时间复杂度：$O(N log N ⋅ K)$。

空间复杂度：$O(N)$。

期望得分：100 分

可以利用splay来将时间复杂度改进到$O( N ( K + log N ) )$。

对这题的评价：5/11