最近正好在写信概的小论文一样的东西所以顺便把这个写了吧
T1:Down The Rabbit Hole
Idea:lxl Solution:lxl Std:lxl Data:lxl
https://www.luogu.org/problemnew/show/P4688
https://www.lydsy.com/JudgeOnline/problem.php?id=4939
可以发现就是求每个数在多个(这里其实可以任意个的)区间里面的出现次数的min
首先想到可以高维莫队,但是复杂度相当地高(主要是常数也很大),所以是过不了的
先考虑如果这三个区间里面每个数最多出现一次的话怎么做,可以想到莫队跑区间搞出每个区间的值域上的bitset,然后and起来,然后count一下就是每个数在这些区间里面出现次数的min了
但是如果有重复的数似乎就没法bitset了?其实是可以的
考虑进行离散化的时候,有一种写法是a[i] = lower_bound( b + 1 , b + n + 1 , a[i] ) - b这样的,相当于给出现次数为x的数留下了x个位置
先离散化,假设数x离散化后的位置是y,然后x出现z次
那么y,y+1…y+z-1这些位置都是x的
莫队维护区间bitset的时候
假设区间中y出现了w次
则我们把y,y+1…y+w-1这些位置填上1
y+w…y+z-1这些位置填上0
比如1 1 1 3 3 3 5 5 5 5 7离散化之后:
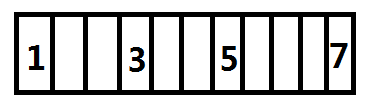
然后跑莫队维护区间的bitset,这个时候把每个数放到其离散化后对应的位置开始第一个非空的位置,这样每个数就是连在一起的了,就像这样:
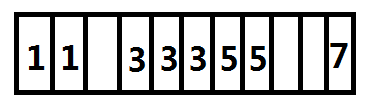
然后我们把每次查询对应的区间的这样的bitset and起来然后count一下就得到了每个数在这些区间中出现次数的min,然后差不多就得到答案了
注意到存下$3 \times 10^5$个长为$10^5$的bitset是一件对空间很毒瘤的事情,所以要分几组跑莫队,不过由于bitset是瓶颈所以这里对时间复杂度和实际运行时间没什么影响
时间复杂度$O( nm/w )$,空间复杂度$O( nm/w )$
对这题的评价:3/11
T2:It's My Own Invention
Idea:lxl改编 Solution:lxl Std:lxl Data:lxl
https://www.luogu.org/problemnew/show/P4689
https://www.lydsy.com/JudgeOnline/problem.php?id=4940
这题的题目名有一种嘲讽的意味(因为这题不是我自己的发明)
来源是一个cf题,然后好像当时被人搬到了SNOI,然后我看了看题感觉还行就改编了一下(其实就是套了个壳子什么的never mind)
发现这个是一个换根然后查子树的问题,这个是一个非常经典的套路——就是假的换根,答案可以被差分为原DFS序上的区间信息
然后查询[l1,r1],[l2,r2]可以按二维前缀和差分为
可以差分为:
F(l1,r1,l2,r2)=F(1,r1,1,r2)-F(1,l1-1,1,r2)-F(1,r1,1,l2-1)+F(1,l1-1,1,l2-1)

这样都变成了前缀的区间之间的贡献
然后就可以在这个上面跑莫队了
这个题m=5e5,然后这个差分会导致最多差分出9个询问
询问最后有5e6个左右,排序的O( mlogm )比较慢
可以考虑对莫队的询问进行基数排序
时间复杂度$O( n \sqrt m + m )$,空间复杂度$O( n + m )$
对这题的评价:3.5/11
T3:Looking Glass Insect
Idea:lxl Solution:lxl Std:lxl Data:lxl
https://www.luogu.org/problemnew/solution/P4690
https://www.lydsy.com/JudgeOnline/problem.php?id=4941
区间染色是有一个均摊性质的
每次区间染色,最多在左端点,右端点处产生两个新的颜色段

所以由于区间染色每次最多只会增加$O( 1 )$个连续颜色段,用平衡树维护所有连续段即可
均摊的颜色段插入删除次数$O( n + m )$
考虑维护每个点与其颜色相同的前驱
发现一个颜色连续段里面除了第一个点以外,后面的点i的前驱都是i-1
用树套树/分治维护,于是这个颜色段的变化可以$O( log^2n )$维护
时间复杂度$O( ( n + m ) log^2n )$,空间复杂度$O( n + m )$
这题不同写法导致的常数可能差5倍(我最开始的写法就是这样的),所以比较诡异,顺便这题细节挺多的(小声)
对这题的评价:4/11
这套题也就这样了(大概是我两年前出的题了吧所以难度很一般),如果大家有兴趣去看看也好吧(不过感觉已经有些过时了)
忘记放可爱的妹子的图片了:


 鄂公网安备 42010202000505 号
鄂公网安备 42010202000505 号