我信概写了3000字才写了一半(老老实实写ML和AI多好啊)
T1:いろとりどりのセカイ(Version3)
Idea:lxl Solution:lxl Std:lxl Data:lxl
https://www.luogu.org/problemnew/solution/P4117
https://www.lydsy.com/JudgeOnline/problem.php?id=5143
http://codeforces.com/problemset/problem/896/E
"突刺贯穿的第二分块" (妈呀这名字好中二啊(谁叫我要用日本轻小说中的东西命名真是作死))
这题的来源比较神奇,大概是csy搬了一个全局大于x的减x,查kth什么的题,然后我想把这个出区间上
然后直接出会得到一个$O( n \sqrt n logn )$的废物,当时想了很久都没想到什么trick能做值域1e9的情况(有没有人教教我啊)
然后改了改发现值域1e5是可以做的就出了出来
考虑分块,可以发现每块的最大值总是不增的
总的所有块的最大值和当块大小为$O( \sqrt n )$时为$O( n \sqrt n )$
考虑怎么利用这个性质
可以发现:假设区间所有大于x的减x,最大值为v
这个操作等价于把区间中所有数减x,之后小于x的再加x
当$v > x \times 2$时,可以把所有$[1,x]$内的数合并到$[x+1,x \times 2]$上
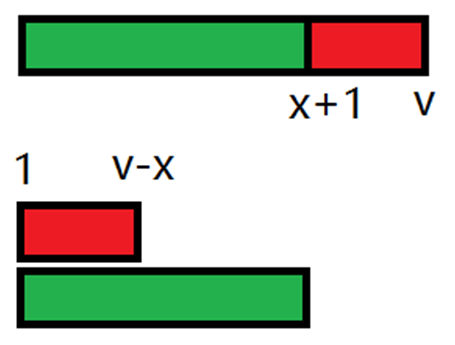
当$v \le x \times 2$时,可以把所有$[x+1,v]$内的数合并到$[1,v-x]$上
如果$v > x \times 2$
我们用$O( x ) \times O( Data Structure )$ 的代价使得块内的最大值减少了$O( x )$
如果$v \le x \times 2$
我们用$O( v - x ) \times O( Data Structure )$ 的代价使得块内的最大值减少了$O( v - x )$
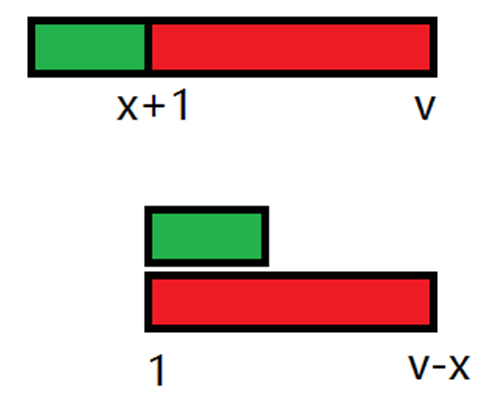
所以要用一个数据结构支持:
$O( 1 )$把块内值为x的全部变成$x+v$
$O( \sqrt n )$求出块内经过大量操作后,每个数的值
第一种是整块操作的时候要用
第二种是重构零散块的时候要用
维护这个有很多种方法
可以每块维护一个值域上的链表
1.定义f[i][j]为第i块里面所有值为j的数的下标的链表
区间所有x变成x+v即link( x , x + v )
然后维护一下块内可能出现的所有数
每次重构的时候即遍历所有可能出现的数,然后遍历其中真正出现的数的链表即可
不过链表常数巨大。。。
这个应该跑的很慢
2.可以每块每个值维护一个vector
然后启发式合并这个vector
这个做法由于对缓存友好,所以会跑的快一些
3.可以用一个并查集维护
这个并查集由于只支持:
merge( x , y )
for( i = 1 ; i <= sqrtn ; i++ ) find( i )
所以复杂度是$O( 1 )$的并查集
本质上和链表的做法是差不多的,不过常数好很多
如果认为值域和n同阶的话(本来也是这样设计的)
时间复杂度$O( (n + m) \sqrt n )$,空间复杂度$O( n \sqrt n )$,可以使用逐块处理的trick把空间复杂度降低到 $O( n + m )$。
顺便这题的Version4是查询区间rank,我记得当时我用当时感觉挺厉害的trick做到了和现在一样的复杂度不过感觉不practical所以没有挂出来
对这题的评价:6/11

T2:終末なにしてますか?忙しいですか?救ってもらっていいですか?(Version6)
Idea:lxl&zyz Solution:ccz Std:lxl Data:lxl
https://www.luogu.org/problemnew/show/P4680
https://www.lydsy.com/JudgeOnline/problem.php?id=5144
"深浅值藏的第六分块" (妈呀这名字好中二啊(谁叫我要用日本轻小说中的东西命名真是作死))
这题好像是当时zyz在某群里面问全局加区间最大子段和怎么做,然后我当时也只会$O( n \sqrt n )$的暴力做法(菜的扣脚)
然后NOI的时候突然想起来然后去问ccz,然后ccz秒出了一个$O( nlog^2n )$的做法,然后我NOI就挂了所以我就没去管这题了
然后我在学文化课养老的时候突然发现有人在bzoj上挂了一个区间加区间最大子段和。。我当时的心情大概就是:\吐血
https://www.lydsy.com/JudgeOnline/problem.php?id=5089
然后发现和我是一样的做法,但是我觉得很不服(明明是我先出的题,怎么就(虽然没挂出来所以其实不能算先出吧))
去和ccz聊了聊,发现区间加区间最大子段和可以做到$O( n \sqrt nlogn)$,然后又想了想发现可以做到$O( n \sqrt n )$(ccz太强了)
先考虑全局加区间最大子段和怎么做
考虑用线段树维护区间的一个分段函数,这个分段函数其实也就是个半平面交
定义
cur -> L()为cur节点内部的左端最大前缀和的一个分段函数
cur -> R()为cur节点内部的右端最大后缀和的一个分段函数
cur -> MID()为cur节点内部的最大子段和的一个分段函数
cur -> L(x)代表cur节点整体被加了x后其最大前缀和
cur -> R(x)代表cur节点整体被加了x后其最大后缀和
cur -> MID(x)代表cur节点整体被加了x后其最大子段和
我们显然有
cur -> L(x) = max( cur -> left -> L(x) , cur -> right -> L(x) + cur -> left -> sum );
cur -> R(x) = max( cur -> left -> R(x) + cur -> right -> sum , cur -> right -> R(x) );
cur -> MID(x) = max( cur -> left -> MID(x) , cur -> right -> MID(x) , cur -> left -> R(x) + cur -> right -> L(x) );
由于两个段数分别为a和b的分段函数取max和加起来得到的分段函数最多有a+b段
所以我们可以递归建线段树,然后由儿子归并得到其的分段函数
这里总复杂度是$O( nlogn )$的(带一个大常数)
这个其实和不带修改的线段树查询区间最大子段和类似,不过我们维护的是关于这个点被加了多少的一个分段函数从而计算出当前的最大前缀,最大后缀,最大子段和
然后考虑怎么拓展到区间加
如果强上分块的话复杂度是$O( n \sqrt (nlogn) )$的(实测应该会被卡)
发现我们这个线段树其实只是一个分治结构而已,不涉及到大量在上面的查询操作
每次重构零散块的时候,可以发现每层只用重构操作边界上的$O( 1 )$个节点,而不用重构整个线段树
于是重构复杂度是$O( \sqrt n + \sqrt n / 2 + \sqrt n / 4 + ... ) = O( \sqrt n )$
于是做到了
时间复杂度$O( (n + m) \sqrt n )$,空间复杂度$O( nlogn )$
据说用什么闵可夫斯基和可以做到同样的复杂度但是好写一些常数也小一些?反正我不会
上述题解是针对Version5,也就是说区间加正数来做的,对于区间加任意数,我们考虑对每个块离线进行基数排序,注意逐块处理,这样就可以通过 $O( (n + m) \sqrt n )$ 次操作转化为区间加正数的问题了。
离线逐块处理可以让空间复杂度变成 $O( n )$。
时间复杂度$O( (n + m) \sqrt n )$,空间复杂度$O( n )$
P.S这题我写的极其恶心写了一周(虽然就是每天逃几节课来写的)
对这题的评价:7.5/11

T3:未来日記(Version2)
Idea:fdy Solution:fdy&lxl Std:lxl&csy Data:lxl
https://www.luogu.org/problemnew/show/P4119
https://www.lydsy.com/JudgeOnline/problem.php?id=5145
http://acm.hdu.edu.cn/showproblem.php?pid=6079
"望月悲叹的最初分块" (妈呀这名字好中二啊(谁叫我要用日本轻小说中的东西命名真是作死))
这个是这个系列中第一个被出出来的题,当时给了多校(然后的确没人做出来耶),然后被搬到了毛营(然后还是没人做出来耶)
这个是我同学出的,不是我出的(当时问我我也不会这题来着),来源似乎是有个$cdqz$高新校区的小朋友看错了一个cf题,然后被加强造出来的
这里就直接挂csy的题解了,和我的不太一样,但是大概思路还是差不多的,我的做法是和T1有点类似的维护方法
先考虑如何求区间第$k$小值。对序列和权值都进行分块,设$b_{i,j}$表示前$j$块中权值在$i$块内的数字个数,$c_{i,j}$表示前$j$块中数字$i$的出现次数。那么对于一个询问$[l,r]$,首先将零碎部分的贡献加入到临时数组$tb$和$tc$中,然后枚举答案位于哪一块,确定位于哪一块之后再暴力枚举答案即可在$O( \sqrt n )$的时间内求出区间第$k$小值。
接着考虑如何实现区间$[l,r]$内$x$变成$y$的功能。显然对于零碎的两块,可以直接暴力重构整块。对于中间的每个整块,如果某一块不含$x$,那么无视这一块;否则如果这一块不含$y$,那么只需要将$x$映射成$y$;否则这一块既有$x$又有$y$,这意味着$x$与$y$之间发生了合并,不妨直接暴力重构整块。因为有$c$数组,我们可以在$O(1)$的时间内知道某一块是否有某个数。
考虑什么情况下会发生重构,也就是一个块内发生了一次合并的时候。一开始长度为$n$的序列会提供$O(n)$次合并的机会,而每次修改会对零碎的两块各提供一次机会,故总合并次数不超过$O(n + m)$,因此当发生合并时直接重构并不会影响复杂度。
那么现在每块中的转换情况只可能是一条条互不相交的链,只需要记录每个初值转换后是什么,以及每个现值对应哪个初值即可。遇到查询的时候,我们需要知道零碎部分每个位置的值,不妨直接重构那两块,然后遍历一遍原数组aa即可得到每个位置的值。
在修改的时候,还需要同步维护$b$和$c$数组,因为只涉及两个权值,因此暴力修改$j$这一维也是可以承受的。
总时间复杂度$O((n + m)\sqrt n )$,空间复杂度$O( n \sqrt n )$
对这题的评价:8.5/11


 鄂公网安备 42010202000505 号
鄂公网安备 42010202000505 号